Tempos de Exposição - Goodman HTS
Autor: David Sanmartim - SOAR/LNA (soar.suporte@lna.br)
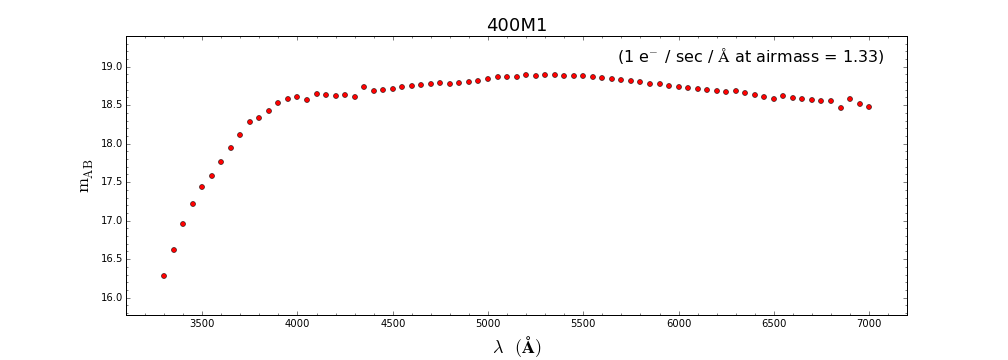
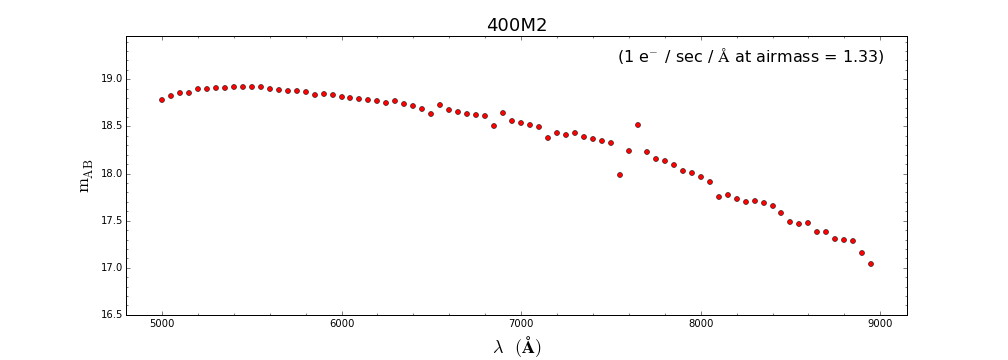
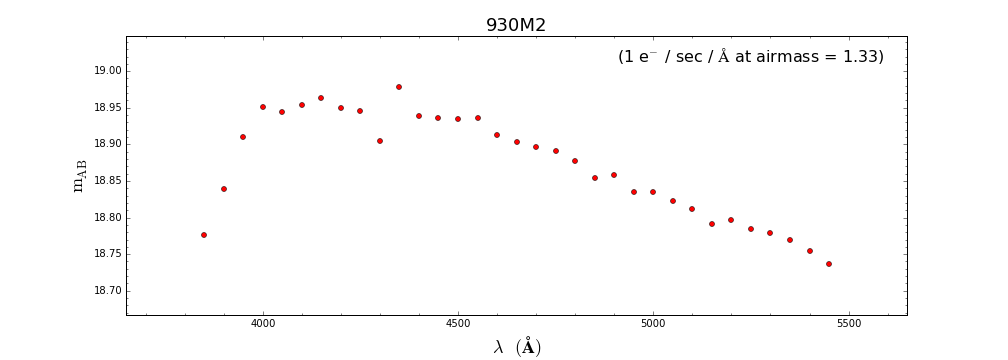
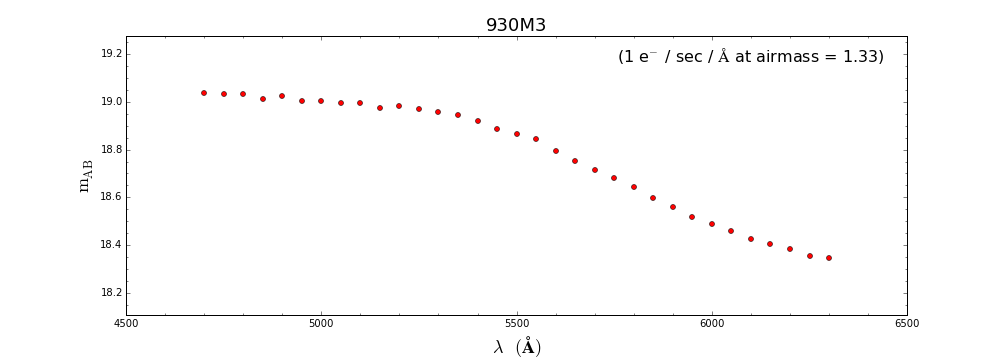
Com a finalidade de substituir a antiga calculadora de tempo do espectrógrafo Goodman, estamos disponibilizando este guia simplificado de uma primeira versão daquilo que deverá ser a nova calculadora de tempo desse instrumento. A partir de observações de uma estrela padrão (tipo A) obtidas em uma noite com iluminação da lua de ~50%, apresentamos abaixo uma série de figuras com a magnitute $m_\rm{AB}$ esperada quando a fonte emite um fluxo de 1 e-/seg/A. Alguns exemplos mostram como utilizar essas figuras para estimar o tempo de exposição requerido a fim de que se obtenha a razão sinal-ruido (SNR) desejada. Os resultados apresentados nesse guia são para as redes de 400 e 930 l/mm, em configurações que cobrem toda a faixa espectral do ótico. Essas estimativas podem ser extrapoladas para outras redes através da respectivas curvas de eficiência.
As figuras apresentadas abaixo baseiam-se em observações espectroscópicas obtidas através de uma fenda de 10.0" de largura e seeing de
$\approx$1.0", de modo que não há perda de luz na fenda. Perdas de luz devem ser consideradas no caso em que a largura da fenda é comparável ao seeing.
Por exemplo, quando usa-se usando uma fenda cuja largura é igual ao seeing, cerca de 25% da luz advinda de um objeto pontual é perdida. O fator de
transmissão $T_\rm {slit}$ ao longo do eixo de dispersão pode ser estimado a partir da seguinte equação:
$$T_\rm{slit} = erf \left[ \dfrac{\frac{slit}{2}}{\sqrt{2} \frac{seeing}{2.35482}} \right], $$
onde $slit$ é a largura da fenda em arcsec e $seeing$ é o valor efetivo do seeing também em $arcsec$. A tabela abaixo mostra o fator de trasmissão
e de perda ($L_\rm{s}=1-T_\rm{s}$) quando a largura da fenda é duas vezes maior que o seeing, igual e 2/3 do valor de seeing:
Slit (arcsec)
Seeing (arcsec)
$T_s$
$L_s$
2
1
0.98
0.02
2
2
0.76
0.24
2
3
0.57
0.43
Rede 400 l/mm
Considerando que as figuras fornecem a magnitude $m_\rm{AB}$ esperada para uma fluxo de 1 e-/seg/A, podemos utilizá-las para estimar
a taxa de contagens esperada pora uma objeto de magnitue m$_\lambda$ (para objetos extendidos, utiliza-se a magnitude integrada). A partir disso,
podemos então estimar o tempo de integração necessário para obter o SNR desejado. Os exemplos abaixo mostram como se pode encontrar a estimativa do tempo de exposição para objetos com magnitudes
V=15.0 and V=18.0:
Fluxo do objeto: V=15 mag
SNR desejado: 100 por pixel
(i.e. ~ 10000 e-/pixel, uma vez que estamos usanso a seguinte aproximação $\rm{SNR} \sim \sqrt{\rm{N}}$ )
Escala de dispersão: 1.0 A/pixel (rede 400 l/mm sem binagem espectral
[aqui para outras redes])
Slit, Seeing, Airmass: seeing=0.8" slit=1.03" (\(T_{\rm slit} = 0.87\))
airmass=1.33
Contagens em ~5500A: 1 e-/sec/A * 1.0 A/pixel * 10^(0.4*(18.8-15.0)) * 0.87 = 28.82 e-/pixel/sec
Texp requerido:
100**2 e-/pixel / 28.82 e-/pixel/sec $\approx\,$ 347 sec.
Considerando a mesma configuração instrumental e condições observacionais para um objeto de magnitude V=18.0, o tempo requerido
para obter o mesmo SNR de ~ 100/pixel aumentará para ~92 min:
Fluxo do objeto: V=18.0 mag
SNR desejado: 100 per pixel (i.e. ~ 10000 e-/pixel)
Escala de dispersão: 1.0 A/pixel (rede 400 l/mm sem binagem espectral)
Slit, Seeing, Airmass: seeing=0.8" slit=1.03" (\(T_{\rm slit} = 0.87\)) airmass=1.33
Contagens em ~5500A: 1 e-/sec/A * 1.0 A/pixel * 10^(0.4*(18.8-18.0)) * 0.87 = 1.82 e-/pixel/sec
Texp requerido: 100**2 e-/pixel / 1.82 e-/pixel/sec $\approx\,$ 5495 sec. $\approx\,$ 91.6 min.
É importante ter em mente que as estimativas acima referem-se ao SNR que será obtido após integrar-se o fluxo ao longo da direção espacial do detector (i.e. para o espectro extraído). Para objetos muito fracos, essas estimativas começam a divergir do valor real, uma vez que o fluxo de fundo (sky backgroung) será comparável
fluxo da fonte. Se o fluxo da fonte for comparável à corrente de dark do CDD (0.0003 e/pixel/seg para o Goodman), as estimativas de tempo também estarão
sendo subestimadas.
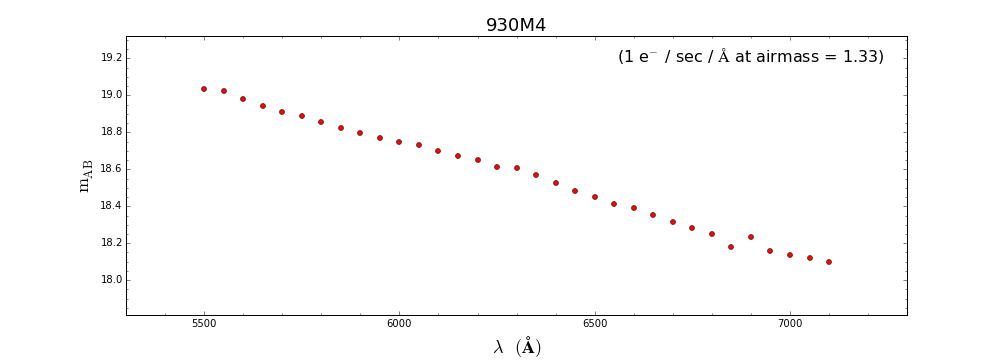
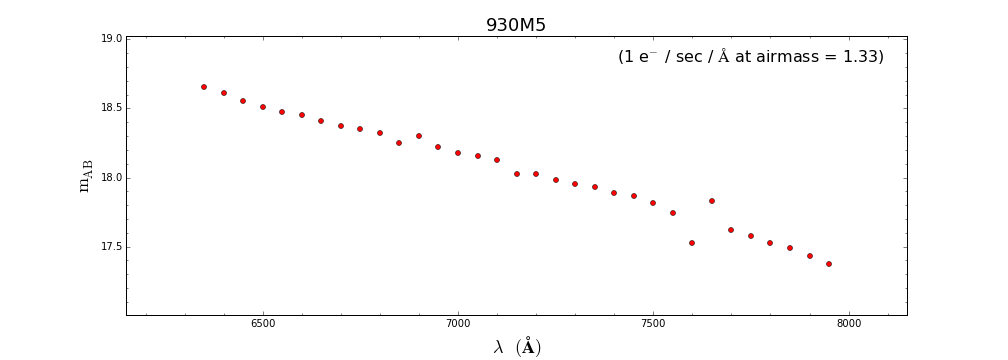
Rede 930 l/mm
Aqui repetem-se os mesmo cálculos para a rede/modo 930M3. Nesse modo, pode-se alcançar um SNR de ~100 (em ~5500 A) para um objeto de
magnitude V=15.0 através de um tempo de exposição de ~ 826 seg.:
Fluxo do objeto: V=15 mag
SNR desejado: 100 per pixel (i.e. ~ 10000 e-/pixel)
Escala de dispersão: 0.42 A/pixel (rede 930 l/mm sem binagem espectral [aqui para outras redes])
Slit, Seeing, Airmass: seeing=0.8" slit=1.03" (\(T_{\rm slit} = 0.87\)) airmass=1.33
Contagens em ~5500A: 1 e-/sec/A * 0.42 A/pixel * 10^(0.4*(18.8-15.0)) * 0.87 = 12.1 e-/pixel/sec
Texp requerido: 100**2 e-/pixel / 12.1 e-/pixel/sec $\approx\,$ 826 sec.